Frank Reilly and Value Scales Part 3

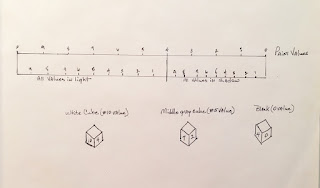
The above shows the value scale we used to find the values of our three cubes from the previous post. I have added the half tones and how they fit on this scale. Half-tones are just what they describe, half dark and half light. So if value 4 is the separation of light and dark you go out 5 units on the light side from value 4 on our scale and 5 units on the shadow side. This is where the half tones would lie. Draw an arrow straight upward to find the paint value. 

 

 

 

Here is a photo of my cubes but remember this time I'm not copying the values. I'm using the set values in the diagram about. 

 

 

 

Here is the painted result of my plotted value structure using Reilly's method in my diagram above. I found the half-tone values by using the objects local value. Let's use the #5 value cube as an example. Where is #5 on my half tone scale? Move the arrow straight upward to the paint scale. It's about value 4.5.  That is now the plotted half-tone value of the top of the #5 cube.  

I do think the blocks turned out looking pretty realistic but going forward I need to work on getting my background to better correspond with the lighting I'm using. As always step back from your work constantly to adjust things accordingly. I'm really happy to have learned a little about how this works and think I will continue my study of the Reilly method. I think it will help with planning values and using relationships in my work not just copying them.  It sure has made me see thru this experiment what is happening with objects in light and shade and the difference is the 'local' value of the object, not the object's color.  The local (home) value and the type and position of the light are, as Reilly states, is THE most important when trying to capture nature, not the local color.

Frank Reilly and Value Scales Part 2

                                                                                                                     

 

I found some of my answers I think studying these 2 excellent books (above),  Jack Faragasso, Students Guide to Painting (hard to find a copy) and A. Dorian, Values for Pictures Worth a Thousand Words (Amazon).  Both of these books teach the Reilly's system of light and shade and the way he plotted value systematically on a value scale depending on the quality and direction of the light source. 

To review, here is what we have learned so far:

A.  Nature's values are limitless

B.  Your medium of choice only has a certain value range compared to nature (0il paint has limited value range)

C.  You can't always just copy natures values like I did in part 1 of this post

So how do we create naturalistic effects with the limited value range of any medium?

According to Reilly the answer is to use value ratios.  And here is an example of what he taught and how the two resource books above demonstrate and how he plotted or planned his values. 

 Let's illustrate this: 

The value scale (above) is divided at the 4th value. (Reilly divided it at 4 with normal 'form light'.  If 

the light was more intense you could divide at #5.  You can get the books to study his explanations of the different lighting conditions). Everything in the light will be between 10 and 4. Everything in   shadow will be between 4 and 0. Now I want to point out an obvious fact from looking at the above diagram and per the Reilly books.  It is at the 4th value that a white object is in shadow and that a black object is in the light. 

Using the 3 cubes (#10 white cube, a #5 mid-value cube, and a # 0 black cube) set up in the shadow box with 'form lighting' creates objects in direct light, in half tone (half light and half shadow), and in shadow (no direct light).  But let's forget the half tones (the tops of the cubes) for the moment to simplify things.  Concentrating just on the light side and the shadow sides of these cubes let's find the paint values using the scales above.  Simply project a line upward to find the paint value from the light and shadow scales. 

Let's start with the #5 value cube. What is the paint value on the light side above # 5 (hint: draw line straight up).  Value 7!  And now what is the paint value above 5 on the shadow side?   Value 2!  Now the white cube. What is the paint value on the light side for #10?  Value 10!  What is the paint value of #10 in shadow?  Right!  Value 4!!  Black cube which is a zero value is where on the light side?  Value 4!!  And on the shadow side is 0!  Good!

This is a simple method of  keeping your objects value within a corresponding paint ratio. Say you are painting a lemon with a local value of say 8. Where does 8 fall on the above light scale?  Value 9 or near!  Where does value 8 fall on the shadow scale?  Value 31/4 or near!  Now this is very simplified explanation of what I have determined so far in studying this method.  I'm going to determine how to plot the half tones (tops of the cubes) and then I'm going to 

paint the cubes to see if these values make them look realistic.